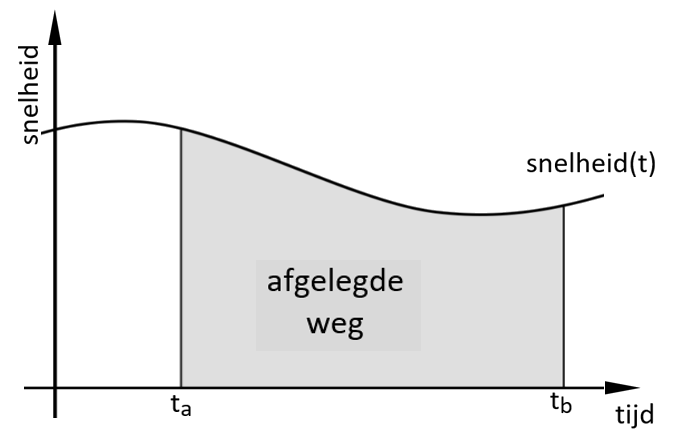
Integreren

Integreren is het optellen van kleine stukjes tot een totaal, bijvoorbeeld de oppervlakte onder een grafiek. De oppervlakte onder de snelheidsfunctie kan men opgebouwd denken uit allemaal smalle kolommetjes met breedte ∆t. De hoogte van het kolommetje wordt gegeven door de snelheid v(t) die de trein op dat tijdstip t heeft. Aangezien snelheid (m/s) maal tijd (s) een afstand (m) is, geldt dat de oppervlakte van ieder kolommetje een stukje afgelegde weg is, namelijk   ∆weg =  v(t) x  ∆t. De gehele oppervlakte onder de snelheidsgrafiek is de optelling van alle stukjes ∆weg. Dat is dan de totaal afgelegde weg.

Differentiëren

Differentiëren is het bepalen van de verandering. In een willekeurig punt op de kromme kan men een raaklijn aan de kromme tekenen. Hoe steiler de raaklijn, hoe groter de verandering van de functiewaarde op dat punt is. Gaat de raaklijn omhoog, dan is de verandering positief. Gaat de raaklijn omlaag, dan is de verandering negatief. De helling van de raaklijn aan de snelheidsfunctie geeft dus aan hoeveel de snelheid op dat punt toeneemt (of afneemt). De verandering van de snelheid is de versnelling. Dus de versnelling wordt gevonden door de snelheidsfunctie te differentiëren.

Hoofdstelling van de integraalrekening

Differentiëren en integreren zijn elkaars inverse, elkaars omgekeerde bewerking. Dit is de hoofdstelling van de integraalrekening.

Met het integreren van de snelheidsfunctie vinden we de verplaatsing (afgelegde weg). Dus door de verplaatsingsfunctie te differentiëren vinden we weer de snelheid.

      

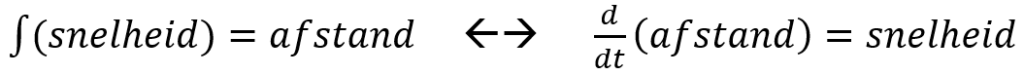
Met het differentiëren van de snelheidsfunctie vinden we de versnelling. Dus door de versnellingsfunctie te integreren vinden we weer de snelheid.

        

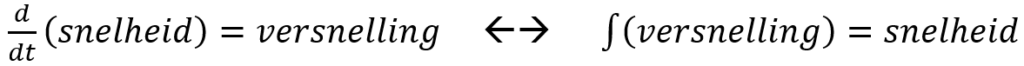
Helling

In het dagelijkse leven betekent ‘helling’ de hoek van een lijn met de horizon. De tangens van deze hoek bepaalt de versnelling. In de wiskunde wordt met ‘helling’ meestal al de tangens van de hellingshoek bedoeld. Een ander woord daarvoor is richtingscoëfficiënt. We komen ook de term ‘hellingsgraad’ tegen uitgedrukt als een percentage. Vooral om de steilheid van een weg aan te geven, belangrijk om te weten als je met je volgepakte caravan door bergdorpjes rijdt.
Een hellingsgraad van 10% betekent dat de verticale verplaatsing 10% is van de horizontale verplaatsting. Grofweg dat je voor iedere 10 m die je rijdt, je 1 m stijgt, of daalt.

Een helling van 10% correspondeert met een hoek van 6^o. Op verkeersborden wordt, ongeacht het percentage dat erbij staat, de steile helling of de gevaarlijke daling standaard als een hoek van 30^o afgebeeld. Dit is een zwaar overdreven, want 30^o correspondeert met een helling van 58%. Maar de overdrijving is noodzakelijk. Want een realistische weergave van een helling van 10%, dus een hoek van 6^o, zou waarschijnlijk niet als steil of gevaarlijk herkend worden door de voorbijrazende verkeersdeelnemers.

Controle van de dimensies

Bij het opstellen van een formule is het altijd belangrijk te controleren dat de fysische dimensie in het linkerlid gelijk is aan die in het rechterlid.

Er staat in het gedicht dat het oppervlak onder de grafiek de afgelegde weg voorstelt. De dimensie van een afgelegde weg is [m]. Hoe kan [m] de dimensie zijn van het oppervlak onder de grafiek? Een oppervlakte is altijd iets in de vorm van hoogte maal breedte. De hoogte (langs de verticale as) is hier een snelheid, we kijken immers naar een snelheidsfunctie. Daarvan is de dimensie [m/s]. De breedte (langs de horizontale as) is de tijd. Daarvan is de dimensie [s]. De dimensie van het oppervlak onder de snelheidsfunctie is dus [m/s  x  s] = [m].

De dimensie van een versnelling is [m/s²]. Er staat in het gedicht dat de tangens van de helling de versnelling is. De tangens van de hellingshoek is de overstaande zijde gedeeld door de aanliggende zijde. De overstaande zijde is een snelheid, dus [m/s]. De aanliggende zijde is tijd, dus [s]. De dimensie van de tangens van de hellingshoek is dus [m/s / s] = [m/s²].